Statistics -

Normal Distribution

Leave a Comment / Statistics / By dsaihub.com / 17 August 2023

All you need to know about Normal Distribution

Imagine a bell-shaped curve that appears over and over in different areas like math science and even in everyday life. This curve is called the normal distribution, or sometimes the Gaussian distribution. It’s a special way to understand how numbers tend to group together. This concept is super important because it helps us make sense of data and predict how things behave in various situations. It is a type of continuous probability distribution for a real-valued random variable and is one of the most important distributions in statistics and the natural sciences.

Characteristics of the Normal Distribution

Symmetry: The normal distribution is symmetric around its mean, with the shape of the distribution identical on either side of the mean.
Mean, Median and Mode: In a perfectly normal distribution, the mean (average), median (middle value) and mode (most frequent value) are all equal and located at the center of the distribution.
Bell-shaped curve: The distribution has a distinct bell shape, which is where the alternative name “bell curve” originates. The bell curve is wide in the middle and tapers off at the ends.
68–95–99.7 Rule: This rule, also known as the empirical rule, states that for a normal distribution, about 68% of the data falls within one standard deviation of the mean, 95% of the data falls within two standard deviations and approximately 99.7% falls within three standard deviations.

What are the properties of normal distributions?

The normal distribution is a bell-shaped curve that is symmetric around the mean, which is denoted by the symbol μ. This means that if we draw a vertical line through the center of the curve at the mean, the area to the left of the line is equal to the area to the right of the line.

Since the total area under the curve of a normal distribution is equal to 1, this implies that the probability of a randomly chosen value being above the mean is equal to the probability of it being below the mean.

For example, if the mean of a normal distribution is 50 and the standard deviation is 10, then the probability of getting a value between 40 and 50 is the same as the probability of getting a value between 50 and 60.

This is because the distribution is symmetric around the mean, and the areas under the curve on either side of the mean are equal.

This property of the normal distribution has many important implications in statistics and data analysis. It allows us to make predictions and calculate probabilities based on the distribution of values around the mean, and it forms the basis for many statistical tests and models.

The standard deviation σ determines the spread or variability of the distribution. As the standard deviation increases, the distribution becomes wider. The normal distribution has many useful properties, such as the fact that 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations.

The standard deviation σ is a measure of the spread or variability of the values in a normal distribution. Specifically, it tells us how much the values in the distribution vary from the mean μ.

If the standard deviation is small, then the values in the distribution are tightly clustered around the mean, and the distribution is narrow. Conversely, if the standard deviation is large, then the values in the distribution are more spread out and the distribution is wider.

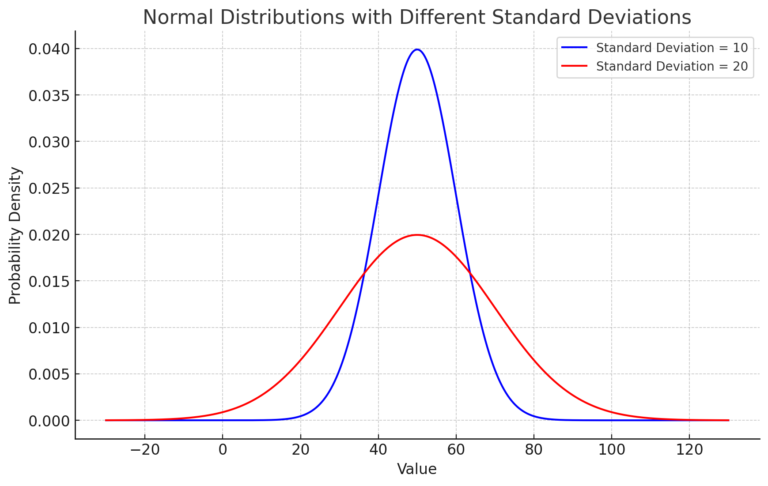
Here’s the graph depicting two normal distributions:

The blue curve represents the distribution with a standard deviation of $10$ . You can see that its values are mostly concentrated around the mean of $50$ , primarily between 4 and .
The red curve represents the distribution with a standard deviation of $20$ . This distribution has a broader spread of values around the mean.

As expected, the distribution with a larger standard deviation is wider, indicating greater variability in the data.

The standard deviation is an important parameter in understanding and analyzing data. It can help us identify outliers or unusual values in a dataset, and it is used in many statistical tests and models to quantify the uncertainty or variability in our measurements or estimates.

The total area under the curve of a normal distribution is equal to 1, which means that the probability of any event occurring is always between 0 and 1

Researchers frequently employ a normal distribution to model the behavior of numerous random variables, such as individuals’ heights or weights within a population.

This characteristic goes by the term “normalization condition.” It guarantees that the overall probability of all potential event outcomes equals 1. In simpler words, the curve’s area represents the cumulative probability of all conceivable outcomes, and this probability consistently ranges between 0 and 1.

In statistical analysis, the normal distribution finds frequent use in estimating the probability of a specific event taking place. By calculating the area under the curve between two points on the distribution, we can determine the probability of an event falling within that range. For example, if we want to know the probability of a person’s height falling between 5’6″ and 6’0″, we can use the normal distribution to calculate this probability.

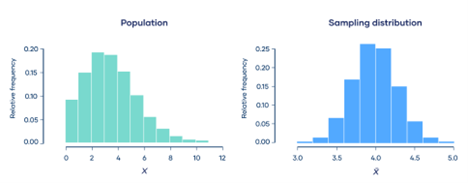
Central limit theorem

It states that the sum or average of a large number of independent and identically distributed random variables tends to follow a normal distribution.

The central limit theorem is a fundamental concept in probability theory and statistics. It states that, under certain conditions, the sum or average of a large number of independent and identically distributed (i.i.d.) random variables tends to follow a normal distribution, even if the individual variables themselves are not normally distributed.

The conditions required for the central limit theorem to hold are:

The random variables must be independent and identically distributed (i.i.d.).
The sample size must be sufficiently large (usually, n ≥ 30).
The random variables must have finite mean and variance.

When these conditions are met, the distribution of the sample mean or sum will be approximately normal, regardless of the underlying distribution of the individual variables. This is particularly useful in practical applications, where the individual variables may have complex and unknown distributions, but the properties of the sample mean or sum can be easily calculated using the normal distribution.

The central limit theorem has important applications in many fields, including finance, physics, engineering and social sciences. It provides a theoretical justification for using statistical inference techniques, such as hypothesis testing and confidence intervals, based on the assumption of normality.

Testing for Normality

Testing for normality is crucial before making assumptions and applying statistical tests. Various techniques can be used to check this, such as QQ-plots, the Shapiro-Wilk test and the Kolmogorov-Smirnov test.

A QQ-plot, or quantile-quantile plot, compares two probability distributions by plotting their quantiles against each other. If the data follows a normal distribution, the points in the QQ-plot will approximately lie on the line y = x.

The Shapiro-Wilk test and the Kolmogorov-Smirnov test are statistical methods used to examine whether a dataset adheres to a specific expected pattern. In both tests, the null hypothesis assumes that the data originates from a population with a known distribution. When the computed p-value falls below the predetermined significance level (usually 0.05), this leads to the rejection of the null hypothesis, indicating that the data does not exhibit characteristics of a normal distribution.

When Data Is Not Normally Distributed

There are many scenarios where data may not follow a normal distribution. For instance, economies often exhibit right-skewed income distributions, where many individuals earn a small amount of money, and only a few earn a substantial sum. In such scenarios, practitioners turn to alternatives to standard methods. They employ non-parametric statistical tests that avoid assuming a specific data distribution. Examples include the Wilcoxon signed-rank test for matched pairs of observations and the Mann-Whitney U test for independent observations.

Applications of the Normal Distribution

It is commonly utilized in both natural and social sciences as a means to represent random variables with real values when the exact nature of their distributions is unknown. It serves as a good approximation for a variety of phenomena, including:

Test Scores: Educational systems often assume that student performance follows a pattern similar to the bell-shaped curve. This simplifies grouping students into categories like “above average,” “average,” or “below average.”
Measurements: Physical attributes such as height, weight, or blood pressure within a group of individuals tend to exhibit a similar bell-shaped pattern.
Quality Control: Numerous manufacturing and business processes adopt this curve to assess variations and ensure quality standards.
Stock Market Returns: In the realm of finance, the returns on stocks or portfolios frequently exhibit a propensity towards a bell-shaped curve pattern.

The normal distribution is not just a cornerstone of statistics; it is a fundamental tool that permeates many scientific disciplines and everyday applications. Its universal nature allows us to make sense of patterns and behaviors in diverse fields, from education and healthcare to manufacturing and finance.

Understanding its characteristics, uses, and importance can greatly enhance our understanding of the world. As we continue to gather and analyze data, the normal distribution will undoubtedly remain a valuable tool, guiding us to the path of new discoveries and insights.

Hypothesis Testing

Leave a Comment / Statistics / By dsaihub.com / 6 July 2023

Hypothesis testing is a powerful statistical tool that enables researchers and analysts to draw meaningful conclusions from data. Whether you’re a scientist conducting experiments, a business professional analyzing market trends, or a student working on a research project, understanding hypothesis testing is crucial for making informed decisions based on evidence.
In this practical guide, we will demystify the process of hypothesis testing and provide you with a step-by-step framework to confidently apply this technique in your own work.

Understanding Hypotheses

Null Hypothesis (H0): The null hypothesis is the default assumption in hypothesis testing. It states that there is no significant difference, effect, or relationship between variables or conditions being studied. The null hypothesis is typically denoted as H0.
Alternative Hypothesis (Ha): The alternative hypothesis is the counterpart to the null hypothesis. It proposes a specific difference, effect, or relationship between variables or conditions being studied. The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting that there is simply a difference without specifying the direction. The alternative hypothesis is denoted as Ha.
H0: “There is no significant difference in pain relief between the new drug and the standard drug.”
Ha: “The new drug provides greater pain relief compared to the standard drug.”
Significance Level (α): A predetermined threshold to determine criteria for accepting or rejecting the null hypothesis. It represents the maximum acceptable probability of making a Type I error (wrongly rejecting the null hypothesis). Commonly used levels are 0.05 (5%) and 0.01 (1%).
Critical Region: The range of values of the test statistic that would lead to rejecting the null hypothesis. If the calculated test statistic falls within the critical region, the null hypothesis is rejected.

One-Tailed Test: In a one-tailed test, you would predict a specific direction of the effect. Let’s say you predict that the new exercise program will result in greater weight loss.

Your null hypothesis (H0) would be that there is no significant difference in weight loss between the two programs. The alternative hypothesis (Ha) would be that the new program leads to more weight loss.

By conducting a one-tailed test, you focus on whether the weight loss with the new program is significantly greater, without considering the possibility of it being less. The critical region would be located in one tail of the bell-shaped curve, and the p-value would be calculated accordingly.

If the p-value is smaller than the chosen significance level, you would reject the null hypothesis in favor of the alternative hypothesis, indicating that the new exercise program leads to statistically significant weight loss.

Two-Tailed Test: In a two-tailed test, you would not have a specific directional prediction. Let’s say you’re simply interested in whether there is any significant difference in weight loss between the two programs.

Your null hypothesis (H0) would be that there is no significant difference, and the alternative hypothesis (Ha) would be that there is a difference (without specifying the direction).

By conducting a two-tailed test, you consider the possibility of weight loss being greater or less with the new program. The critical region would be split between both tails of the bell-shaped curve, and the p-value would be calculated for both sides. If the p-value for either direction is smaller than the chosen significance level, you would reject the null hypothesis in favor of the alternative hypothesis, indicating that there is a statistically significant difference in weight loss between the programs.

In summary, a one-tailed test is used when there is a specific directional prediction, focusing on that particular effect or relationship. A two-tailed test is used when there is no specific prediction or when both directions of the effect are of interest. The critical region and p-value are determined based on the type of test, with the critical region located in the relevant tail(s) of the bell-shaped curve. Understanding these concepts helps in selecting the appropriate test and interpreting the results accurately in hypothesis testing.

Types of Tests

In hypothesis testing, different types of tests are used depending on the research question and the type of data being analyzed. Each type of test is designed to address specific research scenarios and make appropriate statistical comparisons.

Here are some common types of hypothesis tests:

T-tests: T-tests are used to compare means between two groups. They are appropriate when the data follow a roughly normal distribution and the variances of the two groups are assumed to be equal or can be approximated as equal.
Chi-square tests: Chi-square tests are used to examine the association between categorical variables. They assess whether the observed frequencies differ significantly from the expected frequencies under the assumption of independence.
Analysis of Variance (ANOVA): ANOVA is used to compare means between two or more groups. It determines whether there are significant differences in means across multiple categories or levels of an independent variable.
Regression Analysis: Regression analysis is used to examine the relationship between a dependent variable and one or more independent variables. It assesses whether there is a statistically significant linear relationship between the variables.
Non-parametric Tests: Non-parametric tests, such as the Mann-Whitney U test or the Wilcoxon signed-rank test, are used when the data do not meet the assumptions of parametric tests (e.g., normality, equal variances).

The choice of the appropriate test depends on the research question, the nature of the data, and the assumptions underlying each test. It is essential to consider the characteristics of the data and select a test that is most appropriate for the research scenario.

Significance Level and Critical Region

Significance Level (α): A predetermined threshold to determine criteria for accepting or rejecting the null hypothesis. It represents the maximum acceptable probability of making a Type I error (wrongly rejecting the null hypothesis). Commonly used levels are 0.05 (5%) and 0.01 (1%).
Critical Region: The range of values of the test statistic that would lead to rejecting the null hypothesis. If the calculated test statistic falls within the critical region, the null hypothesis is rejected.

Type I and Type II Errors:

Type I error: Occurs when the null hypothesis is wrongly rejected.
Type II error: Occurs when the null hypothesis is not rejected, even though there is a significant effect or difference.

The probability of a Type II error is denoted as β (beta) and is influenced by factors such as sample size, effect size, and the chosen significance level. Lowering the significance level increases the probability of a Type II error.

How to interpret the results of hypothesis testing

Interpreting results involves comparing the obtained p-value with the chosen significance level.
If the p-value is smaller than the significance level, it suggests that the data provide evidence to reject the null hypothesis.
If the p-value is greater than the significance level, it indicates that there is insufficient evidence to reject the null hypothesis.

Steps for hypothesis testing

Formulate the Hypotheses: Define the research question and create null and alternative hypotheses.
Choose the Significance Level: Determine the threshold for rejecting the null hypothesis.
Select the Test Statistic: Choose a statistical method to assess the evidence against the null hypothesis.
Collect and Analyze the Data: Gather data, calculate the test statistic using the chosen method.
Determine the Critical Region and P-value: Identify the range of values leading to null hypothesis rejection or calculate the p-value.
Make a Decision and Draw Conclusions: Decide whether to reject the null hypothesis based on the critical region or p-value.
Interpret and Report Results: Explain the findings, including the decision made, supporting evidence, and any limitations or assumptions.

These steps provide a framework for conducting hypothesis testing and drawing meaningful conclusions from data.

It is important to note that hypothesis testing is not without challenges. Researchers should be mindful of potential pitfalls, such as misinterpreting p-values, inappropriate significance levels, and assumptions that need to be met. By being aware of these considerations, researchers can conduct hypothesis testing with greater accuracy and reliability.

Hypothesis testing is a powerful tool for drawing meaningful conclusions from data. This guide has provided an overview of the key concepts involved, including formulating hypotheses, different types of tests, significance level and critical region, interpreting results, and the steps involved in hypothesis testing.

While we have covered important aspects of it, there are additional topics, such as assumptions, that require further exploration. Assumptions include factors like independence, normality, and equal variances, which impact the validity of results. Exploring specialized resources and academic literature will provide a deeper understanding of these assumptions and their implications.

In our future articles, delving into the assumptions and their effects will enhance your understanding of hypothesis testing. By considering these assumptions and their validity, you can conduct hypothesis testing with greater accuracy and make informed decisions based on reliable evidence.

Understanding Inferential Statistics

Leave a Comment / Statistics / By dsaihub.com / 6 July 2023

Unveiling The Secrets Behind Data Analysis using Inferential Statistics

In the vast field of data analysis, inferential statistics plays a crucial role in extracting important insights from collected data. It enables us to draw conclusions about a population based on a sample, providing a solid foundation for decision-making and hypothesis testing. In this article, we will delve into the fascinating realm of inferential statistics, exploring its key concepts, methods, and applications.

What is Inferential Statistics?

Inferential statistics is a field within statistics that focuses on drawing conclusions about a population by examining data from a sample. It allows researchers to draw conclusions, make predictions, and test hypotheses based on the observed sample. By using probability theory and statistical techniques, inferential statistics helps us generalize findings from the sample to the larger population.

Sampling and Sampling Distributions

To perform inferential statistics, researchers typically collect a sample from a larger population of interest. The sample should be representative and selected using appropriate sampling techniques. Once the sample is obtained, various statistical measures and techniques are applied to analyze the data. Central to inferential statistics is the concept of sampling distributions, which provide valuable insights into the behavior of sample statistics.

Estimation

Estimation is a fundamental aspect of inferential statistics. It involves estimating unknown population parameters based on sample statistics.

Point estimation involves using a single value (e.g., sample mean) to estimate the population parameter (e.g., population mean).

Interval estimation, on the other hand, provides a range of plausible values within which the population parameter is likely to fall, along with a level of confidence.

Hypothesis Testing

Hypothesis testing is a powerful tool in inferential statistics used to make decisions or draw conclusions about a population based on sample data. It involves formulating a null hypothesis (H0) and an alternative hypothesis (Ha), selecting an appropriate significance level, and conducting statistical tests to either reject or fail to reject the null hypothesis. The p-value, which represents the probability of obtaining the observed data under the null hypothesis, is a crucial component in hypothesis testing.

Common Inferential Statistical Techniques

a. Student’s t-test: This test is used to compare means between two independent groups and determine if the difference is statistically significant.

b. Analysis of Variance (ANOVA): ANOVA allows for the comparison of means among three or more groups to determine if there are significant differences.

c. Chi-square test: This test is used to analyze categorical variables and determine if there is a significant association between them.

d. Regression analysis: Regression analysis explores the relationship between variables and allows for predicting outcomes based on predictor variables.

Inferential statistics is a powerful tool that enables researchers to make inferences, draw conclusions, and make informed decisions based on sample data. It serves as the bridge between sample observations and the larger population, unlocking valuable insights and contributing to knowledge in various domains.

Understanding the key concepts, methods, and applications of inferential statistics is crucial for researchers and data analysts.
By utilizing appropriate sampling techniques, estimation methods, hypothesis testing, and statistical techniques, researchers can derive meaningful conclusions, make evidence-based decisions, and drive advancements in their respective fields.
As technology advances and new methodologies emerge, inferential statistics will continue to play a vital role in data analysis and decision-making processes.

Inferential Statistics	Descriptive Statistics
Employ analytical tools on sample data	Quantify the characteristics of the data
Used to make conclusions about the population	Used to describe a known sample or population
Includes hypothesis testing and regression analysis	Includes measures of central tendency and measures of dispersion
Examples: t-tests, z-tests, linear regression etc.	Examples: variance, range, mean, median etc.

Descriptive Statistics: An Introduction to Basic Measures

Leave a Comment / Statistics / By dsaihub.com / 6 July 2023

Descriptive statistics is a part of statistics that helps us understand and describe the basic features of a dataset. It employs measures of central tendency and measures of dispersion to provide a quantitative summary of data. These measures include mean, median, mode, variance, standard deviation and range, among others. In this article, we will provide a detailed explanation of each of these measures, along with examples to illustrate their practical applications.

Mean

The mean is perhaps the most used measure of central tendency in statistics. It is simply the arithmetic average of a set of values. To calculate the mean, you add up all the values in a dataset and divide by the total number of values.

μ = (Σ xi) / n

Example

Suppose we have a dataset consisting of the following test scores:

85 + 90 + 75 + 95 + 80 + 85 + 90 + 95 + 85 + 90

To calculate the mean, we add up all the values and divide by the 
total number of values:

(85 + 90 + 75 + 95 + 80 + 85 + 90 + 95 + 85 + 90) / 10 = 87

The mean test score in this dataset is 87.

Median

The median is another measure of central tendency. It is the middle value in a dataset when the values are arranged in order of magnitude. When the number of values is even, the median is determined by calculating the average of the two middle values.

Example

Suppose we have a dataset of salaries arranged randomly:

$60,000, $75,000, $65,000,$55,000,$50,000,$70,000

To find the median salary, we first arrange the salaries in order:

$50,000, $55,000, $60,000, $65,000, $70,000, $75,000

Median = ($60,000 + $65,000) / 2

Mode

In a dataset, the mode represents the value that appears most frequently. It can be used to describe the most common value in a dataset. In some cases, there may be more than one mode in a dataset, which means that there are multiple values that occur with the same frequency.

Example

Suppose we have a dataset consisting of the following test scores:
85, 90, 75, 95, 80, 85, 90, 95, 85, 90
In this dataset, the value 90 occurs three times, which makes it the mode of the dataset.

Quartiles

Quartiles divide a dataset into four equal parts, with each part representing 25% of the data. The first quartile (Q1) represents the 25th percentile of the data, the second quartile (Q2) represents the 50th percentile (which is the same as the median), and the third quartile (Q3) represents the 75th percentile of the data. The difference between the third and first quartiles (Q3-Q1) is known as the interquartile range (IQR), which is another measure of variability.

To calculate the quartiles of a dataset, we can first sort the data in ascending order. Then we can use the following formulas:

Q1 = (n+1)/4th value
Q2 = (n+1)/2th value (same as the median)
Q3 = 3(n+1)/4th value

The total number of data points in the dataset is denoted by ‘n’.

In addition to providing information about the central tendency of the data, quartiles and the interquartile range can help to identify potential outliers and can provide additional insights into the distribution of the data.

Example

Considering the same dataset
$50,000, $55,000, $60,000, $65,000, $70,000, $75,000

Q1 = ($55,000 + $60,000) / 2 = $57,500
Q2: ($60,000 + $65,000) / 2 = $62,500
Q3 = ($70,000 + $75,000) / 2 = $72,500

The interquartile range (IQR) can be calculated as Q3 - Q1:
IQR = $72,500 - $57,500 = $15,000

Variance and Standard Deviation

The variance is a measure of the spread or variability of a dataset. It measures the distance of each value in the dataset from the mean. A high variance indicates that the values in the dataset are widely spread out, while a low variance indicates that the values are clustered closely around the mean.

The standard deviation is another measure of the spread or variability of a dataset. It is a square root of the variance. Like the variance, the standard deviation is a useful measure for describing the spread of values in a dataset.

Formula

Standard deviation = sqrt(variance)

Here’s the example table for calculating variance and std deviation with the dataset {4, 6, 8, 10, 12}:

Value (xi)	Mean (μ)	Deviation (xi – μ)	(xi – μ)^2
4	8	-4	16
6	8	-2	4
8	8	0	0
10	8	2	4
12	8	4	16

Now, follow these steps:

Sum the squared deviations: 16 + 4 + 0 + 4 + 16 = 40
Divide the sum of squared deviations by the total number of data points (n) for population variance or (n-1) for sample variance.

For population variance: 40 / 5 = 8
For sample variance: 40 / (5-1) = 40 / 4 = 10
Population standard deviation = sqrt(8) = 2.83
Sample standard deviation = sqrt(10) = 3.16

Range

The range of a dataset is obtained by subtracting the lowest value from the highest value, thus representing the difference between the two. It is a simple measure of the spread of values, but it can be sensitive to extreme values. In some cases, the range may not be a good measure of the spread of values if there are outliers in the dataset.

Formula

range = highest value – lowest value

Example

Suppose we have a dataset consisting of the following test scores:

85, 90, 75, 95, 80, 85, 90, 95, 85, 90

The highest value in this dataset is 95 and the lowest value is 75, so the range is:
95 - 75 = 20

The range of this dataset is 20

Conclusion

Descriptive statistics provides a way to summarize and describe the basic features of a dataset. The measures discussed in this article are fundamental to understanding data and are used extensively in a variety of fields, including science, economics and finance. By understanding these measures, you can gain insights into your own data and make informed decisions based on your analysis.

Welcome to the Fascinating World of Statistics:A Universe of Data

Leave a Comment / Statistics / By dsaihub.com / 5 July 2023

If you’re here, it means you’re interested in the science of statistics, its fascinating applications, and its ever-growing importance in our data-driven world. You’re in the right place. Whether you’re a student, a professional, or just a curious mind, we’re here to shed light on the sometimes mystifying, but always intriguing, world of statistics.

Why is Statistics Important?

Statistics is often seen as the backbone of any data analysis process. It is a powerful tool that allows us to extract meaningful insights from data, understand patterns and make informed decisions. At its core, statistics is about understanding variability and making sense of complex data sets. In an era where we generate quintillions of bytes of data each day, the ability to sift through data, find patterns and make predictions is invaluable. Be it economics, biology, social sciences, psychology or business management, statistics is at the heart of it all. It helps us understand trends, test hypotheses, and predict future occurrences.

Where Can We Use Statistics?

The applications of statistics are wide and varied. Here are a few examples:

In business, statistics is used to analyze consumer behavior, optimize operations, forecast sales, and guide strategic decision-making.
In healthcare, it’s used to understand the effectiveness of treatments, analyze patient data, and predict disease patterns.
In social sciences, it helps to analyze societal trends, understand human behavior, and inform policy decisions.
In sports, statistics is used to evaluate player performance, analyze game strategy, and predict outcomes.
In climate science, it’s used to model climate change, predict weather patterns, and inform environmental policies.

The list goes on, with statistics playing a critical role in fields as diverse as astronomy, agriculture, and even the arts.

Statistics in Machine Learning

Now, let’s talk about one of the most exciting applications of statistics: machine learning.
Machine learning, a subset of artificial intelligence (AI), is all about teaching computers to learn from data and make decisions or predictions.
Statistics is crucial to machine learning because it provides the framework for training models on data, validating model performance, and making predictions. Concepts such as probability theory, regression analysis, and hypothesis testing form the foundational pillars of many machine learning algorithms.

For example, in supervised learning (a type of machine learning), we use statistical methods to fit models to data and predict outcomes. We use regression to predict continuous outcomes (like a house’s price), and classification to predict categorical outcomes (like whether an email is spam or not).

In unsupervised learning, we use statistical techniques to find structure in data. For instance, cluster analysis, a statistical method, is used to group similar data points together.
In reinforcement learning, statistics is used to help machines learn from reward-based systems. The machine uses statistical decision-making to determine the best action to take to maximize reward.

In conclusion, without statistics, there would be no machine learning.

Through this blog, we aim to dive deep into these topics and more, unraveling the complex world of statistics and its many applications. We welcome you to join us on this exciting journey!
Stay tuned for our upcoming posts, and together, let’s explore the infinite universe of statistics!